Sofistik. Concrete. 2nd (3rd) Order Analysis
Расчет железобетонных стержней с учетом продольного изгиба
Теоретические основы
При расчете железобетонных конструкций в СП 63.1330 влияние продольного изгиба на несущую способность осуществляется при помощи коэффициента η. На этот коэффициент умножается эксцентриситет продольной силы. Коэффициент η зависит от соотношения продольной силы и условной критической силы:
$ \eta ={\frac {1}{(1-N/N_{cr})}} $
Ncr зависит от жесткости железобетонного элемента в предельной по прочности стадии и расчетной длины элемента:
$ N_{cr}={\frac {\pi ^{2}\cdot D}{l_{0}^{2}}} $
Жесткость в предельной по прочности стадии зависит от геометрических характеристик сечения, модуля упругости бетона и арматуры, длительности действия нагрузки, относительного эксцентриситета продольной силы см. п. 8.1.15 СП63.13330.
Расчетная длина элемента зависит от длины элемента и граничных условий.
Тестовые задачи
Для определения коэффициента продольного изгиба и критической силы в Sofistik были рассмотрены несколько случаев. Сравнение "ручного" и программного расчета проводилось на железобетонных колоннах в виде консолей и шарнирно-опертых стержней. Геометрические характеристики приведены ниже в таблице:
| № | Геометрические характеристики сечения, материалы | Длина, м | Расчетная схема | Коэф. к расчетной длине | Расчетная длина, м |
| 1 | 300х300мм, B30, 4 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 7 | Консоль | 2 | 14 |
| 2 | 300х300мм, B30, 4 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 7 | Шарнирно-опертая балка | 1 | 7 |
| 3 | ø500мм, B30, 8 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 5 | Консоль | 2 | 10 |
| 4 | ø500мм, B30, 8 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 5 | Шарнирно-опертая балка | 1 | 5 |
| 5 | 400х800мм, B30, 8 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 10 | Консоль | 2 | 20 |
| 6 | 400х800мм, B30, 8 арматурных стержня из ø12мм А500, расст. до ц. арм. 50мм | 10 | Шарнирно-опертая балка | 1 | 10 |
Прикладывалась вертикальная и горизонтальная нагрузки:
| № | Вертикальная нагрузка, LC1, кН | Горизонтальная нагрузка(у консоли на свободном конце, у шарнирно-опертой балки посередине), LC2, кН |
| 1 | 190 | 1 |
| 2 | 190 | 1 |
| 3 | 190 | 10 |
| 4 | 190 | 10 |
| 5 | 190 | 4,5 |
| 6 | 190 | 32 |
В плоскости противоположной плоскости, в которой находится горизонтальная нагрузка балки закреплены

В Sofistik были выполнены следующие расчеты:
Линейный расчет
+PROG ASE urs:9 $ Linear Analysis
HEAD Calculation of forces and moments
PAGE UNII 0
SYST PROB LINE
GRP -
LC 10 TITL 'Line'
LCC 1
LCC 2
LC 1
END
Расчет LC1 необходим, чтобы по нему выполнять расчет устойчивости. Можно воспользоваться стандартной задачей. Усилия не зависят от жесткости.
Расчет устойчивости
+PROG ASE urs:23 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 1
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3001 $ Number of eigenvalues,Storage loadcase number
END
+PROG ASE urs:27.1 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 2
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3002 $ Number of eigenvalues,Storage loadcase number
END
+PROG ASE urs:27.2 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 3
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3003 $ Number of eigenvalues,Storage loadcase number
END
+PROG ASE urs:27.3 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 4
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3004 $ Number of eigenvalues,Storage loadcase number
END
+PROG ASE urs:27.4 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 5
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3005 $ Number of eigenvalues,Storage loadcase number
END
+PROG ASE urs:27.5 $ Buckling Eigenvalues
HEAD Eigenvalues Easy
PAGE UNII 0
ECHO MAT FULL
SYST PLC 1 $ use a primary loadcase
GRP 6
EIGE NEIG 1 ETYP BUCK NITE - MITE - LMIN AUTO LC 3006 $ Number of eigenvalues,Storage loadcase number
END
Задачи разделены, чтобы по каждому стержню получить только первую форму потери устойчивости. Возможно использовать стандартную задачу.
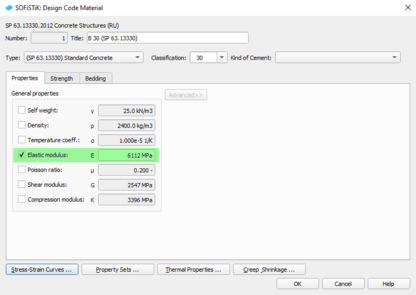
Важно! Для определения критической силы необходимо понижать модуль упругости, чтобы жесткость была равна жесткости железобетонного элемента в предельной по прочности стадии. при помощи GRP FACS это сделать нельзя, поэтому необходимо понижать модуль упругости в материале.
Нелинейный расчет по теории 2-го порядка с ручным понижением жесткости
+PROG ASE urs:9 $ Nonlinear Analysis
HEAD Calculation of forces and moments
PAGE UNII 0
CTRL OPT WARP VAL 0
ECHO FULL FULL
SYST PROB TH2
GRP 1,2 FACS 0.188
GRP 3 FACS 0.112
GRP 4 FACS 0.186
GRP 5 FACS 0.102
GRP 6 FACS 0.074
LC 100 TITL 'Nonl'
LCC 1
LCC 2
END
Жесткости необходимо понижать в соответствии с жесткостью железобетонного элемента в предельной по прочности стадии.
Жесткости в предельной по прочности стадии, коэффициент продольного изгиба, критическая сила были определены при помощи программы для расчета по нелинейной деформационной модели: https://dwg.ru/dnl/13011. Для этого использовались следующие предпосылки:
- характеристики бетона при непродолжительной нагрузке,
- криволинейная диаграмма,
- расчетные характеристики материалов,
- коэффициенты к расчетным сопротивлениям =1,
- отношение моментов внешних сил от действия постоянных и длительных нагрузок к моментам от действия всех нагрузок равно 1.
| № | Начальная жесткость, кНм2 | Жесткость в предельной по прочности стадии, кНм2 | Коэф. понижения жесткости | Модуль упругости, МПа |
| 1 | 22544,3 | 4239,94 | 0,188 | 6112,32 |
| 2 | 22544,3 | 4239,94 | 0,188 | 6112,32 |
| 3 | 102417,4 | 11500 | 0,112 | 3649,28 |
| 4 | 102417,4 | 18999 | 0,186 | 6028,93 |
| 5 | 141537,8 | 14406 | 0,102 | 3307,91 |
| 6 | 141537,8 | 10472 | 0,074 | 2404,59 |
Геометрически и физически нелинейный расчет
+PROG ASE urs:9 $ Nonl + nstr
HEAD Calculation of forces and moments
PAGE UNII 0
CTRL OPT WARP VAL 0
ECHO FULL FULL
SYST PROB TH3 FMAX 0.85 TOL -0.2
NSTR S1 KSV UL KSB UL FMAX 0.85
GRP -
LC 200 TITL 'Nonl + nstr'
LCC 1
LCC 2
END
Результаты расчета
| № | Коэф. продольного изгиба из ручного расчета(в направлении меньшей жесткости) | Коэф. продольного изгиба из Sofistik (вычисляется как отношение изгибающего момента в линейном и геометрически нелинейном расчете). Жесткость понижена вручную | Коэф. продольного изгиба из Sofistik (вычисляется как отношение изгибающего момента в линейном и геометрически нелинейном расчете). Жесткость задается по диаграмме | Критическая сила из ручного расчета, кН | Критическая сила из Sofistik(в стандартной задаче вычисляется коэф. и на него умножается заданная сила. Горизонтальная нагрузка отсутствует) | |||
| 1 | 9,084 | 9,81 | 1,08 | 1,27 | 0,14 | 213 | 207,1 | 0,97 |
| 2 | 1,286 | 1,25 | 0,97 | 1,05 | 0,82 | 854 | 826,5 | 0,97 |
| 3 | 1,201 | 1,17 | 0,98 | 1,07 | 0,89 | 1135 | 1100,1 | 0,97 |
| 4 | 1,026 | 1,02 | 1,00 | 1,01 | 0,98 | 7500 | 7187,7 | 0,96 |
| 5 | 2,148 | 1,98 | 0,92 | 1,66 | 0,77 | 355,5 | 347,7 | 0,98 |
| 6 | 1,225 | 1,19 | 0,97 | 0,93 | 0,76 | 1033,6 | 1008,9 | 0,98 |
Выводы:
- Усилия при геометрически нелинейном расчете очень сильно зависят от жесткости элементов.
- Для соответствия программного и ручного расчетов в расчете устойчивости жесткость необходимо понижать, чтобы она соответствовала жесткости железобетонного элемента в предельной по прочности стадии.
- Для соответствия программного и ручного расчетов при определении коэффициента продольного изгиба жесткость необходимо понижать, чтобы она соответствовала жесткости железобетонного элемента в предельной по прочности стадии.
- Sofistik показал хорошую сходимость при определении коэффициента продольного изгиба и критической силы.
- При расчете физически (по диаграммам) и геометрически нелинейной задачи нет хорошей сходимости в ручными расчетами. Это связано с тем, что фактически элемент не достигает предельной по прочности стадии и его фактическая жесткость больше. С одной стороны, это лучше отражает реальную работу элемента, с другой стороны, это расходится с СП не в запас.
